Psychologists like their analyses like I like my coffee: robusta. Results shouldn’t change too much, no matter which exclusion criteria are applied, which covariates are included, which transformations are applied to the outcome variable.
A simple way to check robustness are, guess what, robustness checks. Change one thing at a time, see what happens (lather, rinse, repeat).
A spacy way to check robustness is multiverse analysis. Here, instead of changing one thing at a time, a list of defensible “model ingredients” is compiled: various outlier criteria, sets of covariates, plausible transformations, etc. Next, all combinations of model ingredients are generated, and the resulting multitude of models are estimated. In an instance of convergent evolution, variations of multiverse analyses have been invented multiple times in different fields. Ranked by the coolness of the names chosen by the respective authors, these include: Multiverse Analysis (Steegen, Tuerlinckx, Gelman and Vanpaemel, 2016; which deservedly has become the hypernym), Vibration of Effects (Patel, Burford, and Ioannidis, 2015, not to be confused with Effects of Vibration, Cubitt, 2012 nsfw), Specification Curve Analysis (Simonsohn, Simmons, & Nelson, 2020), and Computational Multimodel Analysis (Young & Holsteen, 2015).[1]Wolf Vanpaemel noted that he considers Many Analysts analysis an outsourced multiverse analysis and I think that’s sensible. That said, I think in practice there could be some differences because (1) all involved analysts commit to one particular model they consider meaningful and (2) not all model ingredients are combined, so some of the criticism voiced in this blog post does not quite apply.
The multiverse has struck a string chord with psychologists; however, there seems to be some degree of confusion about what these analyses can achieve. Thus, this blog post offers a tiered classification of multiverse analysis. These will include what (I think) the authors of the respective methods intended and what (I think) applied researchers want from the multiverse and what (I think) I think robustness means.
Tier 1: Mülltiverse Analysis
Multiverse analysis sounds really cool and complex and looks fancy, if you add the right type of plot (Fig. 1). Thus, it invites mindless methods opportunism and conformism (see also Theory of Everything). For example, a researcher struggling to make their results appear novel may put a spin on it by throwing a multiverse on top, maybe even claiming that the study contributes to the literature by expanding multiverse analysis to multilevel-mediation dynamic continuous time multilevel latent-growth curves.[2]I have reviewed variations of this. Or they may apply it reflexively, for example, when reviewers raise concerns about the robustness of that post-hoc triple interaction, but then fail to properly integrate the resulting numbers (“look, it’s highly significant in some models!”). Which surely adds some degree of novelty to the literature, but not necessarily robustness.

Figure 1. Can’t outrun the new analysis trend.
Mülltiverse Analysis throws together all sorts of things. Different sets of outlier criteria, different sets of covariates, fancy data transformations, sample splits; including many analytic choices that do not seem particularly sensible. But the presentation of results will almost necessarily imply that all specifications are exchangeable (if some were inherently unpreferrable, why include them in the first place?) and we end up with something like Figure 2.
All in the name of robustness, but we have to ask ourselves: robustness to what? Which leads us to Tier 2, multiverse analysis to assess substantive robustness.

Figure 2. Shiny Gigantamax Garbodor (source).
Tier 2: Multiverse Analysis to Assess Substantive Robustness
The following borrows heavily from Lundberg, Johnson, and Stewart’s (2021) amazing paper titled “What is Your Estimand? Defining the Target Quantity Connects Statistical Evidence to Theory.” It’s the type of paper that makes me wish that I had a time machine so I could travel back and scoop it, or at least travel back and tell younger me how to re-write my papers. You may go read Lundberg et al. now. It provides compelling arguments, clear language and mathematical notation. In contrast, this blog post only provides bad jokes, shoddily edited images and Gen 5 Pokémon references.
To think about substantively meaningful robustness, we first need to think about our theoretical estimand. The theoretical estimand is the central target of our analysis, defined in precise terms that exist outside of statistical models. So, “the coefficient of ice-cream consumption on depression when controlling for Socio-Economic Status” does not count because it only refers to our statistical model. “The effect of ice cream on depression” is a bit better, but imprecise. Now, if we talk about the score on Beck’s depression inventory if one had eaten one reasonably-sized serving of ice cream (3 scoops) minus the score on Beck’s depression inventory if one had drunk a glass of sauerkraut juice, averaged over the population of German psychology undergraduate students, that is even better.[3]For more precision and less stupid examples, check out Hernán and Robins’ excellent free textbook “What If?”, sections 3.4 to 3.6.
Some questions of robustness concern this theoretical estimand. For example, we may want to consider whether the effect also shows up on a different measure of depression; or whether it also shows up averaged over a different subpopulation. This type of robustness may be relevant for the evaluation of our theory if it predicts that effects show up across measures, or across subpopulations.
The theoretical estimand is linked to an empirical estimand via assumptions. This step is very much about conceptual considerations: No amount of empirical data can get rid of those pesky assumptions. For example, if our study is observational and we collected two thousand variables from one million people, we still need to identify a sensible set of covariates based on our assumptions about the causal web. Some questions of robustness concern this link between theoretical estimand and empirical estimand. For example, we may want to consider whether the effect also shows up when including (or excluding) certain covariates, which implies different assumptions about the underlying causal web. This type of robustness is of interest when we are not quite certain about the causal role of certain variables, and want to ensure that conclusions don’t hinge on them.
Lastly, we estimate the empirical estimand with the help of an esteemed estimation strategy. This is where we get into the domain of statistics as psychologists like it, and this is where decision may be (partially) data driven. Do we run a linear regression or some other fancy model? Do we include Likert-scale covariates as dummies or as continuous variables?
So, we got three levels of robustness: Theoretical estimand, linking theoretical and empirical estimand, and estimation strategy. Is multiverse analysis the right tool for any of them?
Considering the theoretical estimand, I’m somewhat skeptical. Changing the theoretical estimand changes the target of the analysis, and multiverse approaches at least strongly imply that all analyses are providing an answer to the same question (e.g., by providing an overall estimate, at least visually). Here, I’d probably prefer to see results reported as traditional “robustness checks”, or even as parallel manuscript sections.
Considering the link between theoretical and empirical estimand, I’m at least as skeptical. Different links imply different sets of assumptions which need to be discussed, and which may greatly vary in plausibility — this doesn’t go well with modes of presentation that somehow that all specifications are exchangeable.[4]Wolf voiced some mild disagreement here and I fully concede that not all visualizations of multiverse analysis imply such exchangeability to the same degree. Plotting the effect estimates as a histogram strongly implies exchangeability; presenting them in a manner that single specifications can still be identified probably less so. That said, even when single specifications can still be identified, I suspect that most readers will take in the multiverse “as a whole” and simply eyeball the whole distribution or the fraction of “significant” estimates. Once again, I’d probably prefer to see results presented as traditional robustness checks, with a thorough discussion of the different sets of assumptions involved.
Considering the estimation strategy, maybe that’s where the multiverse fits best because this stage is less assumption-driven and more data-driven. Then again, if decisions are data-driven that means once again they are not exactly arbitrary. For example, they may involve known trade-offs. Let’s assume we have a confounder that was measured on an ordinal scale. If we have a lot of data, we can include it as a dummy to fully control for its effect.[5] Okay okay, under the unrealistic assumption of no measurement error. If we don’t, we may instead include it as a continuous predictor, which can get us more power but potentially introduces bias if the association between the confounder and the outcome isn’t linear. So once again, the specifications aren’t quite directly comparable.
TL;DR: Multiverse analysis doesn’t quite seem like the right tool to evaluate substantive robustness.
Tier 3: Multiverse Analysis to Assess Robustness to Arbitrary Changes
But when you read the actual papers on the multiverse methods (in particular Steegen et al. or Simonsohn, Simmons, & Nelson), they were never intended to assess substantive robustness, so maybe what I said above misses the point. Both talk about arbitrary decisions in data analysis.
For example, consider the question of whether hurricanes with feminine names cause more deaths (the infamous Hurricanes vs. Himmicanes). Simonsohn et al. list the following types of choices: outlier removal, operationalizating hurricane names’ femininity, operationalizing hurricanes’ strength, type of regression model, and functional form of femininity.[6]The last one happens to be a great name for an art project on gender.
If these choices are really arbitrary, all possible combinations are equally plausible, and presenting them from a bird’s-eye view seems sensible. But are they really arbitrary, as in, either way is equally fine?
The next few sentences sound horribly anal, but I promise this will lead somewhere less cheeky. I looked up why people exclude outliers in the first place and one major concern seems to be incorrect data entry. In that case, outlier removal isn’t that arbitrary — for example, if you know that some data points are impossible, you should exclude them; keeping them isn’t a defensible decision. I’m not a hurricanologist, but I also have to assume that there are better or worse ways to operationalize the strength of hurricanes and the femininity of their names. Considering the usage of negative binomial regression vs. ordinary least squares with the logarithm of death[7]Yet another great name for an art project, or maybe a metal band. as outcome — there is a great answer on Stack Exchange explicating the differences which, at least in theory, don’t seem that trivial.
</anality>
But maybe that’s not really meant by “arbitrary.” Maybe these choices are arbitrary in the sense that a king can arbitrarily rule over his people: what he does actually may matter a great deal, but he doesn’t care that about your arguments regarding the sensibility of beheading every single duck in his kingdom. Other terms used in multiverse methods papers include “defensible” and “justified”, and if you expand these to “defensible in front of the reviewers” and “jusitfied given our (imperfect) knowledge”, maybe that gets closer to the intended meaning:
Yes, removing outliers may sometimes be the right thing to do; but people often don’t care about the specifics; and sometimes we may genuinely not know if something was a data entry error or not. Yes, there may be better or worse ways to operationalize femininity; but in any case we often let subpar measurement procedures pass; and it seems like a bit of an underspecified construct to begin with. Yes, negative binomial vs. OLS with logarithm may be substantively different; but I guess most people don’t know in which ways (I certainly didn’t).
Which leads us back…
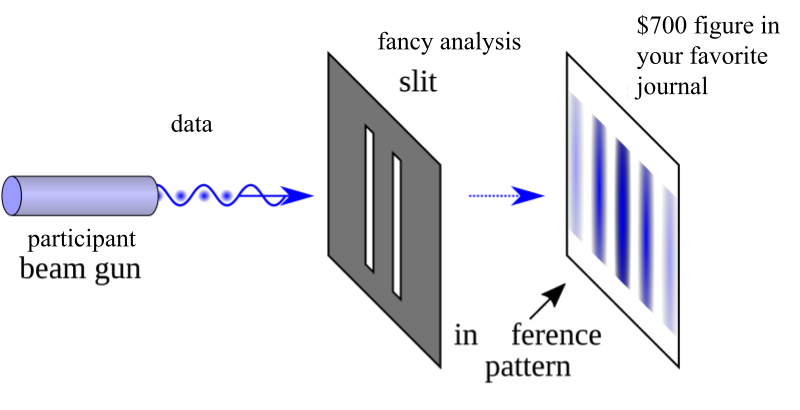
Figure 3. Psychology is hard science.
Tier 4: Mülltiverse Analysis Because in the End, Pretty Much Everything is Arbitrary
Maybe the messiness of the Mülltiverse is appropriate given how analysis decisions are frequently made in psychology. That is, researchers may try a bunch of stuff without being sure whether or not it makes sense, and whether or not it should make a difference at all (been there, done that). If, as original authors, we present a multiverse, we at least are much more transparent about the unknowns. And, as critics, a multiverse may help us figure out whether results could have plausibly resulted from standard data-torturing procedures.
It seems to me that multiverse analysis is often applied in that vein. Imagine there are 1000 ways to analyze the data that would be publishable, all else being equal. Now, if the preferred conclusion of a significant effect only shows up in one particular analysis—what Young and Holsteen call “a knife-edge specification”—it seems fairly safe to dismiss it as a false positive. Any claim to the contrary, and any criticism invoking the possibility of “null-hacking” will need to come up with a very good justification for why all 999 alternative specifications are unsuitable. Such a justification may be possible; but given how psychologists tend to justify their modeling choices and assumption:[8]i.e., not color me skeptical. How likely is it that the one true effect is observable only exactly when the stars align to yield exactly that one out of one-thousand model specifications?
But for other patterns, it’s not that easy. What if the multiverse is ambiguous? There could be substantive variability, which puts us back to considerations of substantive robustness. It could also just be in your head—it’s rather easy to come up with a good story after the fact. The multiverse isn’t necessarily robust to motivated reasoning (but then again, nothing is). What if the multiverse shows unambiguous evidence in favor of the preferred conclusion? That’s a good sign, unless, of course, there is something amiss across model specifications (so we’re back at thinking hard about our estimand); and unless model-ingredients weren’t hand-picked to ensure this outcome. Wouldn’t it be blatantly obvious to spot a p-hacked multiverse? Well, it probably would, for those people who can spot suspicious patterns (such as weird distributions of p values) in the first place; but others might be dazzled into agreement. Which may be one of the perils of multiverse analysis: a false sense of certainty.
Tier 0: Maybe the Real Treasure was the Insights we Gained Along the Way
In the end, the multiverse may prove to be most powerful as a pedagogical tool. Heyman and Vanpaemel (2020) have a great preprint on multiverse in the classroom which partially inspired me to write this blog post. I wouldn’t limit this to classrooms though–in the end, there’s a lot that the field as a whole can learn.
Multiverse analysis can raise awareness of how data analytic flexibility can be exploited. It can also alert us to gaps in our knowledge. Gaps in our knowledge about the underlying causal web: Is including that covariate arbitrary or not? What does it mean if results hinge on it? Gaps in our knowledge about statistics: Can we expect these types of models to return the same answer? Under which conditions would they diverge? Gaps in our knowledge about measurement and conceptualization: Does it make sense to expect the same result for these different operationalizations of the outcome? What does it mean if results vary? We have now closed the loop and are back to the original multiverse paper, in which the authors write: “The real conclusion of the multiverse analysis is that there is a gaping hole in theory or in measurement.”
We can’t expect that mindless multiversing will provide reliable substantive answers if we do not move on and address these gaps. In the end, you can’t brute-force inference with more data and more stats.
Many thanks to Wolf Vanpaemel who provided super helpful feedback on this post, and to Ian Lundberg who ensured I’m not talking nonsense about his paper. Neither of them bears any responsibility for any remaining nonsense. Blame my co-bloggers.
Epilogue: A Little Malte-Verse
“Analyses are arbitrary!”
say Steegen, Tuerlinckx, Gelman, & Vanpaemel,
the psychologist checks if results vary,
in JASP, R, and – yes – Excel.
“By iterating choices,
research quality could be increased!”
The psychologist rejoices,
– “Oh, like, using sour dough vs. yeast?”
“Uh, kinda, but in terms of stats.
You should show your results are robust.”
The psychologists grunts “Rats!”
One more task to earn trust.
Footnotes
| ↑1 | Wolf Vanpaemel noted that he considers Many Analysts analysis an outsourced multiverse analysis and I think that’s sensible. That said, I think in practice there could be some differences because (1) all involved analysts commit to one particular model they consider meaningful and (2) not all model ingredients are combined, so some of the criticism voiced in this blog post does not quite apply. |
|---|---|
| ↑2 | I have reviewed variations of this. |
| ↑3 | For more precision and less stupid examples, check out Hernán and Robins’ excellent free textbook “What If?”, sections 3.4 to 3.6. |
| ↑4 | Wolf voiced some mild disagreement here and I fully concede that not all visualizations of multiverse analysis imply such exchangeability to the same degree. Plotting the effect estimates as a histogram strongly implies exchangeability; presenting them in a manner that single specifications can still be identified probably less so. That said, even when single specifications can still be identified, I suspect that most readers will take in the multiverse “as a whole” and simply eyeball the whole distribution or the fraction of “significant” estimates. |
| ↑5 | Okay okay, under the unrealistic assumption of no measurement error. |
| ↑6 | The last one happens to be a great name for an art project on gender. |
| ↑7 | Yet another great name for an art project, or maybe a metal band. |
| ↑8 | i.e., not |

1 thought on “Mülltiverse Analysis”
Comments are closed.