or
Dear Sanjay
TL;DR: Publication bias is a bitch, but poor hypothesising may be worse.
Estimated reading time: 10 minutes

A few weeks ago I was listening to episode 5 of the Black Goat, flowery thoughts on my mind, when suddenly I heard Sanjay Srivastava say the following words (from minute 37:47):
And this is what I struggle with, right, with Registered Reports and this idea that we should be focusing on process and soundness and all this stuff. If there’s two papers that have equally good methods, that, before I knew the results, I would have said they were equally well-posed questions, but one reports a cure for cancer and the other reports a failed attempt to cure cancer – I’m gonna like the cure for cancer more, and I can’t escape feeling like at some point, you know, that shit matters.
First, a clarification: Sanjay does like Registered Reports (RRs)! He gave the following comment on his comment (meta Sanjay): “Looking at that quote in writing (rather than spoken) and without any context, it might sound like I’m ambivalent about RRs, but that’s not the case. I fully support the RR format and I don’t think what I said is a valid reason not to have them.” The issue is further discussed in a new Black Goat episode.
I have to admit this statement was a bit startling when I first heard it – Sanjay doesn’t like null results? But, but… publication bias! Ok, I should say that I am a bit über-anxious when it comes to this issue. I think that our collective bias against null results is one of the main causes of the replication crisis, and that makes me want everyone to embrace null results like their own children and dance in a circle around them singing Kumbaya.
But Sanjay is right of course – we all want a cure for cancer;[1]Except for nihilists. (There’s nothing to be afraid of, Donny.) we want to find out what is true, not what isn’t. And that is why positive results will always feel more interesting and more important to us than null results. This is the root of publication bias: Every player in the publication system (readers, journal editors, reviewers, authors) is biased against null results. And every player expects every other player to be biased against null results and tries to cater for that to make progress.
Of course there are exceptions – sometimes we don’t buy a certain theory or don’t want it to be true (e.g. because it competes with our own theory). In these cases we can be biased against positive results. But overall, on average, all things being equal, I would say a general bias towards positive findings is a fair assessment of our system and ourselves, and this is what we’ll talk about today.
In this post, I will try to make the case for null results. I’m up against Sanjay Srivastava’s gut feeling, so this better be convincing. Ok, here we go: Four reasons why we should love null results.
1) We are biased against null results
Because we find positive results more important and interesting, we fall prey to motivated reasoning: We will judge studies reporting positive results to be of higher quality than studies reporting null results. We will retrospectively downgrade our impression of the methods of a paper after learning it produced null results. And we will be more motivated to find flaws in the methods, while the methods of papers reporting positive results will get an easier pass.[2]I like the illustration of motivated reasoning by Gilovich (1991), explained here: Evidence in favour of your prior convictions will be examined taking a “Can I believe this?” stance, whereas evidence in opposition to your prior beliefs will be examined taking a “Must I believe this?” stance. The must stance typically gives evidence a much harder time to pass the test.
This means that as soon as we know the results of a study, we are no longer competent judges of the used research methods. But we know that sound methods make and break what we can learn from a study. This is why we absolutely must shield ourselves from judging papers based on or after knowing the results.
In other words: It’s ok to prefer the cancer-cure-finding RR to the non-cancer-cure-finding RR.[3]Well… not really, though. If this leads to better outcomes for authors of positive results (fame, citations, grants), you still select for people who are willing and able to game the remaining gameable aspects of the system. But they have to be RRs, because we are guaranteed to fool ourselves if we base publication decisions on this feeling.
Reason #1: We should love null results to counter our tendency to underestimate their quality.
2) Null results are unpopular because our epistemology sucks
NB: I tried to avoid going down the epistemological and statistical rabbit holes of NHST and instead focus on the practical surface of NHST as it’s commonly used by psychologists, with all the shortcomings this entails.
This section was partly inspired by Daniël Lakens’ recent workshop in Munich, where we looked at the falsifiability of hypotheses in published papers.
I think one reason why null results are unpopular is that they don’t tell us if the hypothesis we are interested in is likely to be false or not.
The most common statistical framework in psychology is null hypothesis significance testing (NHST). We start out with a shiny new hypothesis, Hshinynew, which typically postulates an effect; a difference between conditions or a relationship between variables. But, presumably because we like it so much that we wouldn’t want it to come to any harm, we never actually test it. Instead, we set up and test a null hypothesis (H0) of un-shiny stuff: no effect, no difference or no relationship.[4]Better known as Gigerenzer’s “null ritual” If our test comes up significant, p < .05, we reject H0, accept Hshinynew, and fantasise about how much ice cream we could buy from our hypothetical shiny new grant money. But what happens when p ≥ .05? P-hacking aside: When was the last time you read a paper saying “turns out we were wrong, p > .05″? NHST only tests H0. The p-value says nothing about the probability of Hshinynew being true. A non-significant p-value means that either H0 is true or you simply didn’t have enough power to reject it. In a Bayesian sense, data underlying a non-significant p-value can be strong evidence for the null or it can be entirely inconclusive (and everything in between).
“In science, the only failed experiment is one that does not lead to a conclusion.”
(Mack, 2014, p. 030101-1)
Maybe it’s just me, but I do find strong evidence for H0 interesting. Or, if you’re not a fan of Bayesian thinking: rejecting Hshinynew with a low error rate.[5]These two are not identical of course, but you get the idea. I assume that we don’t reject Hshinynew whenever p ≥ .05 mainly because we like it too much. But we could, and thanks to Neyman & Pearson we would know our error rate (rejecting Hshinynew when it is true): beta, more commonly known as 1-power. With 95% power, you wouldn’t even fool yourself more often when rejecting Hshinynew than when rejecting H0.
There must be a catch, right? Of course there is. Das Leben ist kein Ponyhof, as we say in German (life isn’t a pony farm). As you know from every painful minute spent on the Sample Size Samba, power depends on effect size. With 95% power for detecting dshinynew, you have less than 95% power for detecting anything smaller than dshinynew. So the catch is that we must commit ourselves to defining Hshinynew more narrowly than “something going on” and think about which effect size we expect or are interested in.
I think we could gain some null-result fans back if we set up our hypothesis tests in a way that would allow us to conclude more than “H0 could not be rejected for unknown reasons”. This would of course leave us with a lot less wiggle space to explain how our shiny new hypothesis is still true regardless of our results – in other words, we would have to start doing actual science, and science is hard.
Reason #2: Yeah, I kind of get why you wouldn’t love null results in these messy circumstances. But we could love them more if we explicitly made our alternative hypotheses falsifiable.
3) Null results come before positive results
Back to the beginning of this post: We all want to find positive results. Knowing what’s true is the end goal of this game called scientific research. But most of us agree that knowledge can only be accumulated via falsification. Due to several unfortunate hiccups of the nature of our existence and consciousness, we have no direct access to what is true and real. But we can exclude things that certainly aren’t true and real.
Imagine working on a sudoku – not an easy-peasy one from your grandma’s gossip magazines[6]bracing myself for a shitstorm of angry grannies but one that’s challenging for your smartypants brain. For most of the fields you’ll only be able to figure out the correct number because you can exclude all other numbers. Before you finally find that one number, progress consists in ruling out another number.
Now let’s imagine science as one huge sudoku, the hardest one that ever existed. Let’s say our future depends on scientists figuring it out. And we don’t have much time. What you’d want is a) putting the smartest people of the planet on it, and b) a Google spreadsheet, because Google spreadsheets rock so that they could make use of anyone else’s progress instantly. You would want them to tell each other if they found out that a certain number does not go into a certain field.
Reason #3: We should love null results because they are our stepping stones to positive results, and although we might get lucky sometimes, we can’t just decide to skip that queue.
4) Null results are more informative
The number of true findings in the published literature depends on something significance tests can’t tell us: The base rate of true hypotheses we’re testing. If only a very small fraction of our hypotheses are true, we could always end up with more false positives than true positives (this is one of the main points of Ioannidis’ seminal 2005 paper).
When Felix Schönbrodt and Michael Zehetleitner released this great Shiny app a while ago, I remember having some vivid discussions with Felix about what the rate of true hypotheses in psychology may be. In his very nice accompanying blog post, Felix included a flowchart assuming 30% true hypotheses. At the time I found this grossly pessimistic: Surely our ability to develop hypotheses can’t be worse than a coin flip? We spent years studying psychology! We have theories! We are really smart! I honestly believed that the rate of true hypotheses we study should be at least 60%.
A few months ago, this interesting paper by Johnson, Payne, Want, Asher, & Mandal came out. They re-analysed 73 effects from the RP:P data and tried to model publication bias. I have to admit that I’m not maths-savvy enough to understand their model and judge their method,[7]I tell myself it’s ok because this is published in the Journal of the American Statistical Association. but they estimate that over 700 hypothesis tests were run to produce these 73 significant results. They assume that power for tests of true hypotheses was 75%, and that 7% of the tested hypotheses were true. Seven percent.
Uh, umm… so not 60% then. To be fair to my naive 2015 self: this number refers to all hypothesis tests that were conducted, including p-hacking. That includes the one ANOVA main effect, the other main effect, the interaction effect, the same three tests without outliers, the same six tests with age as covariate, … and so on.


Let’s see what these numbers mean for the rates of true and false findings. If you’re anything like me, you can vaguely remember that the term “PPV” is important for this, but you can’t quite remember what it stands for and that scares you so much that you don’t even want to look at it if you’re honest… For the frightened rabbit in me and maybe in you, I’ve made a wee table to explain the PPV and its siblings NPV, FDR, and FOR.
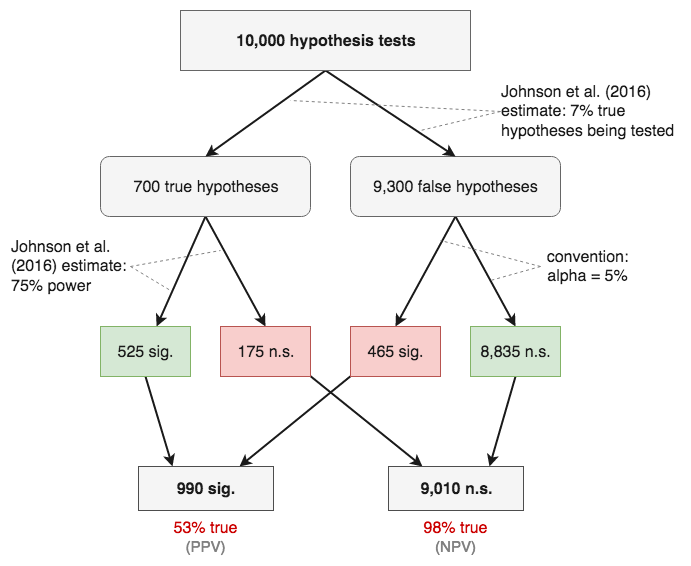
Ok, now we got that out of the way, let’s stick the Johnson et al. numbers into a flowchart. You see that the PPV is shockingly low: Of all significant results, only 53% are true. Wow. I must admit that even after reading Ioannidis (2005) several times, this hadn’t quite sunk in. If the 7% estimate is anywhere near the true rate, that basically means that we can flip a coin any time we see a significant result to estimate if it reflects a true effect.
But I want to draw your attention to the negative predictive value. The chance that a non-significant finding is true is 98%! Isn’t that amazing and heartening? In this scenario, null results are vastly more informative than significant results.
I know what you’re thinking: 7% is ridiculously low. Who knows what those statisticians put into their Club Mate when they calculated this? For those of you who are more like 2015 Anne and think psychologists are really smart, I plotted the PPV and NPV for different levels of power across the whole range of the true hypothesis rate, so you can pick your favourite one. I chose five levels of power: 21% (neuroscience estimate by Button et al., 2013), 75% (Johnson et al. estimate), 80% and 95% (common conventions), and 99% (upper bound of what we can reach).
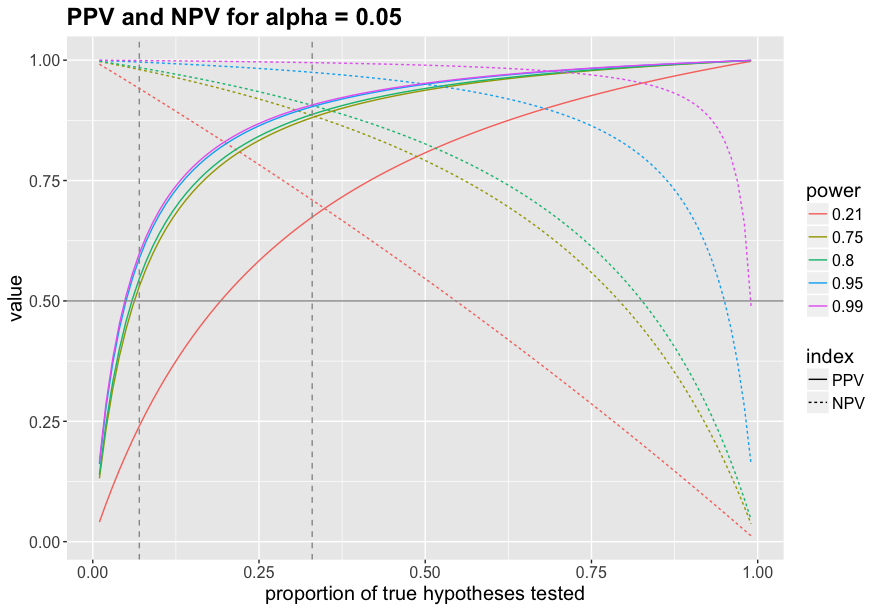
The plot shows two vertical dashed lines: The left one marks 7% true hypotheses, as estimated by Johnson et al. The right one marks the intersection of PPV and NPV for 75% power: This is the point at which significant results become more informative than negative results. That happens when more than 33% of the studied hypotheses are true. So if Johnson et al. are right, we would need to up our game from 7% of true hypotheses to a whopping 33% to get to a point where significant results are as informative as null results!
This is my take-home message: We are probably in a situation where the fact that an effect is significant doesn’t tell us much about whether or not it’s real. But: Non-significant findings likely are correct most of the time – maybe even 98% of the time. Perhaps we should start to take them more seriously.
Reason #4: We should love null results because they are more likely to be true than significant results.
Especially Reason #4 has been quite eye-opening for me and thrown up a host of new questions – is there a way to increase the rate of true hypotheses we’re testing? How much of this is due to bad tests for good hypotheses? Did Johnson et al. get it right? Does it differ across subfields, and if so, in what way? Don’t we have to lower alpha to increase the PPV given this dire outlook? Or go full Bayesian? Should replications become mandatory?[8]In the Johnson et al. scenario, two significant results in a row boost the PPV to 94%.
I have no idea if I managed to shift anyone’s gut feeling the slightest bit. But hey, I tried! Now can we do the whole Kumbaya thing please?
References
Button, K. S., Ioannidis, J. P. A., Mokrysz, C., Nosek, B. A., Flint, J., Robinson, E. S. J., & Munafò, M. R. (2013). Power failure: Why small sample size undermines the reliability of neuroscience. Nature Reviews Neuroscience, 14, 365–376.
Dawson, E., Gilovich, T., & Regan, D. T. (2002). Motivated reasoning and performance on the Wason Selection Task. Personality and Social Psychology Bulletin, 28(10), 1379–1387. doi: 10.1177/014616702236869
Gigerenzer, G. (2004). Mindless statistics. The Journal of Socio-Economics, 33, 587–606.
Gilovich, T. (1991). How we know what isn’t so: The fallibility of human reason in everyday life. New York: Free Press.
Ioannidis, J. P. A. (2005). Why most published research findings are false. PLoS Medicine, 2(8), e124. doi: 10.1371/journal.pmed.0020124
Johnson, V. E., Payne, R. D., Wang, T., Asher, A., & Mandal, S. (2017). On the reproducibility of psychological science. Journal of the American Statistical Association, 112(517), 1-10. doi: 10.1080/01621459.2016.1240079
Mack, C. (2014). In Praise of the Null Result. Journal of Micro/Nanolithography, MEMS, and MOEMS, 13(3), 030101.
Open Science Collaboration (2015). Estimating the reproducibility of psychological science. Science, 349(6251), aac4716.
Footnotes
| ↑1 | Except for nihilists. (There’s nothing to be afraid of, Donny.) |
|---|---|
| ↑2 | I like the illustration of motivated reasoning by Gilovich (1991), explained here: Evidence in favour of your prior convictions will be examined taking a “Can I believe this?” stance, whereas evidence in opposition to your prior beliefs will be examined taking a “Must I believe this?” stance. The must stance typically gives evidence a much harder time to pass the test. |
| ↑3 | Well… not really, though. If this leads to better outcomes for authors of positive results (fame, citations, grants), you still select for people who are willing and able to game the remaining gameable aspects of the system. |
| ↑4 | Better known as Gigerenzer’s “null ritual” |
| ↑5 | These two are not identical of course, but you get the idea. |
| ↑6 | bracing myself for a shitstorm of angry grannies |
| ↑7 | I tell myself it’s ok because this is published in the Journal of the American Statistical Association. |
| ↑8 | In the Johnson et al. scenario, two significant results in a row boost the PPV to 94%. |

Nice post. The way I see it the core of this issue is really that two methodologically equal studies producing opposite results are on the whole just inconclusive evidence. Actually that’s not entirely true: if you take the effect size into account the meta-analysis of both could be quite conclusive. But let’s for the moment just assume that study 1 produce a super-massive and significant effect and study 2 produced a nigh-zero non-significant effect. What that tells you, it is that we haven’t learned very much.
How we should respond to that depends on some other factors. If the experiment was important (e.g. cure for cancer) then we should probably do a third study with an even larger sample size (because studies 1 and 2 were obviously not sensitive enough to detect it reliably). If the experiment is of lesser importance, say, the effect of cognitive load on binocular rivalry dynamics (because that is precisely what happened to us a few years ago) then perhaps you call it a day.
Either way though, you should probably reevaluate carefully if there could have been any difference between studies 1 and 2 that was uncontrolled and that could have been meaningful. I know hidden moderators etc are a bit of a joke these days and they are frequently abused in these debates – but it is just as delusional to think that just because both studies were RRs that they perfectly controlled everything.
Of course, a moderating factor you hypothesise that obliterates your finding will in many case destroy the meaningfulness of your study. In our case, the difference between the original and replication data set was that they used different stimulus equipment and the replication measured eye movements. Thus, the opposite result in the replication *could* have been due to these differences. But if that were true, this would make the phenomenon completely uninteresting because it’s far too volatile to be telling us anything about general perception and cognition. However, in the case of the cancer cure I think even small differences could be important. If the cure works only on one subject group for instance, due to some genetic factor perhaps, I think this is something you surely would want to know about!
Hi Sam, thanks for the comment! I agree that what we make of inconsistent results also depends on the relevance of the research question.
The way I understood Sanjay’s comment was different though: I think it was meant to imply that study 1 and 2 are testing different hypotheses, e.g. “drug A cures cancer” vs “drug B cures cancer”. And we could assume that both results were super convincing, we could even say they are both true – the intuition that study 1 (which found a positive result) would be all over the news and study 2 wouldn’t still holds.
The things you say about different studies on the same hypotheses (or very similar hypotheses) are definitely important though. And I totally agree with you on the moderator issue – just because the argument has been misused as a last resort for drowning theories doesn’t mean that it can never be true. I think it’s probably true very to some degree often or always (and we take that into account when we design our experimental setups).
Ah yes I can see now how Sanjay’s comments could be read that it was about two different cures (and that’s probably what he meant). I definitely see that point. But in the end, I agree with you that knowing that drug B does not cure cancer (assuming it is a well-powered, well-executed study) is also important. After all, if we knew what we were doing it wouldn’t be called research. Discovering a new island is more exciting than sailing endlessly around empty seas – but at least knowing which parts of the sea you have already sailed through usually saves you time until you finally come across that island.
Excellent, thought-provoking piece. Two quick thoughts: the 7% figure is false for most fields and the true figure will depend on your field. However, the logic probably holds with the true figure likely to be in the 1% to 30% range for many areas (at least if we think in terms of non-negligible effects that could be discriminated from noise in reasonable samples). With a second study you can increase the proportion to 53% according to your simulation … So within-paper replication is a useful tool if we can use tools like pre-registration to limit impact of research df.
Sure – I don’t think it’s very fruitful to accept the 7% as a given, especially because it refers to all statistical tests, not necessarily to what we as researchers consider to be a hypothesis. I think it’s important to focus on that discrepancy though and get a better feeling for how statistical hypothesis tests actually relate to our “theoretical” hypotheses.
What does the 53% figure refer to in your case? Using the Johnson et al. estimate, a successful replication of a significant result would raise the PPV to 94%. So yes, one takeaway for me was that replication studies really, really matter. But as you said, preregistration or it didn’t happen 😉 I’d even go as far to demand RRs, because “normal” preregistered studies can still fall victim to self-censorship or publication bias.
I was thinking of the 990 significant effects being followed up by a second study. 53% of this group are true effects. Having an independent replication of an effect under conditions that control researcher df should be fruitful.
Interesting post. I’d like to add a thought. The informativeness of your result hinges on the a-priori probability of your hypothesis. When there are only two houses in the village, it works fine when I tell you where I do NOT live. In a city, this information is pretty useless, but you gain a lot in information when I tell you my address. I presume that information theory formalizes this.
That’s a very nice analogy. And I totally agree with the main message. But the problem is that we’re in a situation where your address can’t be accessed directly. Instead, we have to knock on every door and check if you live there or not. In that scenario, keeping track of every house you don’t live in becomes absolutely crucial to avoid a ton of redundant work (assuming several teams combing through the city).
People hoping to see a fight between us will be disappointed, because I largely agree with the the overarching message of this post about the value of null results. As you note, Alexa, Simine, and I discuss these issues in the most recent episode of The Black Goat (http://bit.ly/2qIvihd). And I have written before about these issues, such as about the importance of designing research so that nulls will be informative (e.g., http://bit.ly/2rswENZ) and how low power affects false discovery rates (http://bit.ly/2qHTqAA).
The slippage, I think, comes in the fact that in the passage you quote, I never said that nulls are not valuable. What I said was that at least some of the time, some kinds of results will be valued more than others. That is about the relative value of some results in comparison to other results (not about any results lacking value in absolute terms). I hope it is not a controversial claim. (Anne, you even say you agree with it, so if I’m wrong and the Twitter mobs comes after me, I’m taking you down with me!).
Why do I think this is an important point, and why do I “struggle” with it? Two reasons.
Reason one, because at some point in the scientific process people are going to be unblinded to the results whether we like it or not, and we have to be prepared to deal with the consequences. A good Registered Report policy will shield the evaluation of a single study (or paper-length package of studies) from results. But that study is part of a larger research program, literature, and field. And after the paper comes out, its reception will be dependent on its results: whether or how much people pay attention to it, remember it, cite it, get inspired to do follow-up studies on it, turn it into applications, etc. Those things, in turn, will have reputational effects for how we evaluate the researcher and the journal. We have to decide if we are okay with that, or if we want to shield those processes too. In fact, the context of the original quote was us talking about how universities evaluate researchers: we were discussing a proposal to do that on “soundness” (which is relatively results-blind) rather than “excellence.” And in the most recent episode we talk about how journals that adopt registered reports will have to rethink the way they use citation-based metrics of success like impact factors, because citations will depend on results and that creates a distorting incentive for journals.
Reason two, and this may be more controversial, is whether results *should* matter at some point in evaluating science. At the level of evaluating individual papers, the case for blinding ourselves to results is strong: it promotes an accurate scientific record, and it shifts the focus of evaluation to the things that researchers can control, which is posing good questions or hypotheses and trying to answer them with sound methods. But in the bigger picture, a lot of science is done in the interest of other goals, like advancing public health, improving educational outcomes, etc. Certainly our funders and other stakeholders will see it that way, though I think many scientists see science as having public value too. So at a close-up, granular level we can shield the evaluation of individual publications from considering results, but at some point in zooming out we are going to end up judging a program of research, a subfield or field, or all of science itself on its positive discoveries. Figuring out where to do that, and how to do that without creating distorting incentives for the process, needs to be part of the conversation too.
I know I’m really late to the party but I couldn’t get myself to reply earlier, either to Sanjay’s original remark nor to Anne’s post, because I’m still unsure whether I’ve thought this through thoroughly enough.
I keep thinking about Sanjay’s original remark in the podcast (although in the follow-up he sometimes seems to me as wishing he would’ve framed or phrased it differently): We want to know the cure for cancer that worked (p .05).
But I don’t think this is true. I’m not a specialist on cancer but I imagine you cannot give all treatments that are supposed to work (at our current state of knowledge) at once, either because they don’t work in conjunction or, more likely, because health insurance won’t pay for them all. Instead, your physician will have to choose. And I certainly want him to know with all the certainty research can give not only which one(s) to choose but which one(s) to safely rule out. My conjecture is: We will never have certain knowledge but if there’s only a set amount of money and there’s uncertainty about the comparative value of different treatments, “discrediting” one of the candidates (in favour of the others) is, to me as a patient, just as valuable as giving credence to another.
And I think this also relates to your two points, Sanjay: I think that research programmes, too, will have value if they can show that something is *not* true. Look at homoeopathy! There is a non-negligible amount of studies and meta-analyses showing positive effects (larger than placebo) of homoeopathic medicine. Now, I myself think homoeopathy is bogus, not least because the theory behind it seems to be nonsense. But if my kid is sick with a rare disease and there’s the choice between two very expensive options that both have very low chances of success, similar low levels of scientific support (yeah, it worked in a few cases and didn’t in a few others) – I would give anything for another very well-powered study; and a trustworthy negative result would give me just as much information to decide between the two as a positive, wouldn’t it?
Yes, it may *seem* that a positive result makes me more sure of my decision. But, in my understanding, that’s a fallacy, at least if we see evidence as a) relative (in the sense of having to decide between options that are mutually exclusive and uncertain) and b) cumulative. So, yes, we *do* need big grants and research programmes for decisively ruling out treatments, much more so if they seem plausible at first. Which homoeopathy of course doesn’t, but there’s another thing: This particular example has garnered so much public attention that even disproving a nonsense theory has a lot of value. (And I have no clue whether you can get good grants for medical research in that area but I sure hope you can!)
Anyway, I’m ranting and I’m not sure it relates to your arguments but I needed to get this out.
(BTW: An interesting, unfortunately German-only, read on this is here: http://harald-walach.de/2016/02/29/die-wiederentdeckung-des-rades-macht-es-selten-runder-homoeopathiekritik-geht-in-eine-neue-runde/ He sounds like he’s pro-homoeopathy at first, but in the course of the article it turns out it’s much more subtle than that. I read him as just being pro-rigor.)